
por Pierre Loidreau
<pierre.loidreau(at)ensta.fr>
Sobre el autor:
Pierre es profesor e investigador en la ENSTA (Ecole
Nationale Supérieure de Techniques Avancées - Escuela
Nacional Superior de Técnicas Avanzadas ). Su campo de investigación son los
"criptosistemas" basados en la teoría de códigos correctores de errores. Practica Linux
a diario... y tenis a menudo.
Taducido al español por:
Roberto Hernando Velasco (homepage)
Contenidos:
|
Introducción a la criptografía

Resumen:
Este artículo se ha publicado en un número especial sobre la seguridad de Linux
Magazine France. El editor, los autores y los traductores han aceptado amablemente que todos
los artículos de ese número especial sean publicados en LinuxFocus. En consecuencia,
LinuxFocus os "ofrecerá" esos artículos a medida que se vayan traduciendo al inglés.
Este resumen se reproducirá en todos los artículos que tengan el mismo origen.
Porqué la criptografía. 2500 años de historia
El origen de la criptografía se remonta sin duda a los orígenes del hombre,
desde que aprendió a comunicarse. Entonces, tuvo que encontrar medios
de asegurar la confidencialidad de una parte de sus comunicaciones. En el antiguo
Egipto, la escritura jugó a veces ese papel. Sin embargo, el primer testimonio
de uso deliberado de métodos técnicos que permitieran cifrar los mensajes
viene de Grecia, sobre el siglo VI antes de Cristo, y se llama "escitalo".
El escitalo era un bastón. El emisor enrollaba una tira de cuero alrededor
del bastón y escribía longitudinalmente sobre el bastón. Después desenrollaba
la tira y la enviaba al destinatario. Sin conocer el diámetro del bastón que había
jugado el papel de clave, era imposible descifrar el mensaje. Más tarde los
ejércitos romanos utilizaron para comunicarse el cifrado de César, consistente en
desplazar el alfabeto tres letras.
Después, durante cerca de 19 siglos, se asiste al desarrollo más o menos
ingenioso de técnicas de cifrado experimentales donde la seguridad residía
esencialmente en la confianza que quisieran darles los usuarios. En el siglo
XIX, Kerchoffs estableció los principios de la criptografía moderna. Uno de los principios
establece que la seguridad de un sistema de cifrado no reside más que
en la clave y no en el procedimiento de cifrado.
En lo sucesivo, concebir sistemas criptográficos debía responder a esos criterios.
Sin embargo, todavia les faltaba a esos sistemas unos cimientos matemáticos suficientes que proveyeran
utilidades para medir y cuantificar su resistencia a eventuales ataques y, por qué
no, encontrar el "Santo Grial" de la criptografía: el sistema incondicionalmente seguro.
En 1948 y 1949 dos artículos de Claude Shannon, "Teoría Matemática de la Comunicación" y
sobre todo "La Teoría de la Comunicación de los Sistemas Secretos" dieron los
cimientos científicos a la criptografía borrando tanto vanas promesas como falsos prejuicios. Shannon
probó que el cifrado de Vernam introducido algunas decenas de años antes --todavía
llamado one-time pad-- era el único sistema incondicionalmente seguro. Sin embargo
el sistema era impracticable. Es por lo que hoy en día la evaluación de la seguridad
de un sistema se interesa principalmente en la seguridad computacional.
Se dice que
un sistema de cifrado de clave secreta es seguro si ningún ataque conocido de
menor complejidad que la búsqueda exhaustiva sobre el espacio de claves ofrece mejores
resultados que ésta.
AES (Advanced Encryption Standard, Norma de Encriptación Avanzada)
Muy recientemente, en octubre de 2000, el NIST (National Institute of
Standards and Technology, Instituto Nacional de Estándares y Tecnología) eligió,
entre 15 candidatos, un nuevo estándar de cifrado con
clave secreta para
reemplazar al viejo DES, debido a que el tamaño de las claves se había vuelto demasiado
pequeño. El algoritmo elegido para convertirse en el AES es el Rijndael, cuyo nombre
viene del de sus creadores, Rijmen y Daemen.
Éste es un sistema de cifrado llamado "por bloques" ya que los mensajes están cifrados por
bloques completos, que aquí son de 128 bits. Hay varias versiones del sistema utilizando
claves de 128, 192 o 256 bits. Como información apuntar que el DES cifra bloques de 64 bits
con una clave de 56 bits solamente. El triple DES utilizaba normalmente hasta entonces
cifras con bloques de 64 bits con una clave de 112 bits.
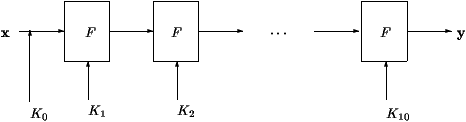
Figura 1: Iteraciones del AES
El principio de funcionamiento del AES está descrito en la figura 1. En primer lugar,
se añade bit a bit al mensaje la clave secreta K0 .
Después, como para todos los algoritmos de cifrado por bloques, se itera una función
F, parametrizada por subclaves que se obtienen de la clave maestra mediante
un algoritmo de expansión de claves.
En el caso de AES, se itera 10 veces la función F.
- La figura 2 describe cómo se itera la función F para cifrar.
Se toma como entrada bloques de 128 bits repartidos en 16 octetos. Antes de
nada, se aplica a cada octeto la misma permutación S. Seguidamente, se
aplica a los 16 octetos una segunda permutación P. Entonces al resultado
obtenido se le añade bit a bit la subclave de 128 bits obtenida por el algoritmo de expansión
de clave.
- El algoritmo de expansión de clave permite calcular la clave Ki
de la i-ésima iteración en función de la subclave Ki-1 de la
(i-1)-ésima iteración, siendo K0 la clave
secreta. Esto se describe en la figura 3. Los 16 octetos de la clave Ki-1
se toman de 4 en 4. Los últimos 4 octetos se permutan usando una permutación S,
que es la misma que se utiliza para permutar los bits de cada octeto de la función. Después
se suma al primer octeto del nuevo conjunto el elemento ai.
Este elemento es un octeto que depende del número i de la iteración considerada.
Por último, para obtener Ki, se añade bit a bit los
4 octetos obtenidos a los 4 primeros octetos de Ki-1,
después el resultado obtenido es agregado a los 4 octetos siguientes y así sucesivamente.
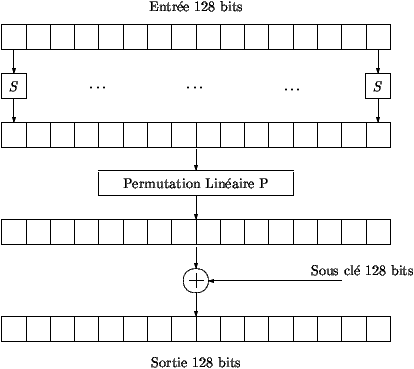
Figura 2: Función F
Veamos brevemente cómo se construyen las permutaciones y a qué corresponde la
constante ai.
Técnicamente y por simplicidad, un octeto se puede considerar como un elemento
de un conjunto con 256 elementos llamado cuerpo finito, sobre el que existen todo
tipo de operaciones simples, entre otras las operaciones de adición, producto e
inversión. La permutación S anteriormente mencionada corresponde a la
inversión sobre este conjunto. La permutación P está especificada como
una operación muy simple, implementándose fácilmente. El elemento ai
corresponde a elevar a la potencia i un elemento del cuerpo. Estas
consideraciones permiten implementar AES de forma muy eficaz.
Como el AES no comprende más que operaciones muy simples sobre los octetos
se tienen dos ventajas enormes:
- incluso la implrmentación por software de AES es extremadamente rápida.
Por ejemplo, una implementación en C++ sobre un Pentium a 200MHz permite
cifrar a 70Mbits/s;
- la resistencia de AES a los criptoanálisis diferencial y lineal no depende
de la elección de S-Cajas como en el DES, que habían sido sospechosas de haber
sido amañadas por la NSA. En efecto, todas las operaciones efectuadas son operaciones
simples.
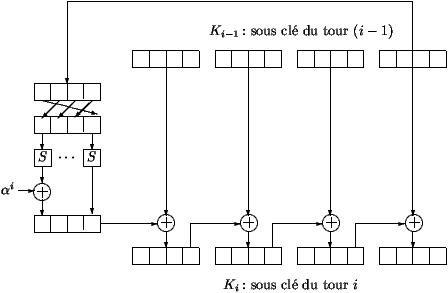
Figura 3: Algoritmo de expansión de claves
Criptografía de clave pública
En 1975 Diffie y Hellman publicaron un artículo llamado "New Directions in
Cryptography" (Nuevas direcciones en Criptografía) que tuvo el efecto
de una bomba en la comunidad de los criptógrafos, introduciendo
el concepto de criptografía de clave pública. Los algoritmos de cifrado
con clave secreta (o clave privada), los únicos conocidos hasta entonces, ya no satisfacían
las nuevas necesidades que aparecían paralelamente a la explosión de
nuevos medios de comunicación muy impersonales -- como por ejemplo, el desarrollo de las redes
de comunicaciones.
La solución completamente revolucionaria que propusieron fue introducir
la noción de función de una sola vía con trampa, o trapdoor one-way function (también
conocida como función de un sentido irreversible).
Es una función que se calcula fácilmente en un sentido, pero que es
computacionalmente imposible de invertir si no se conoce un secreto
llamado trampa, aunque la función sea conocida por todos.
Entonces la clave pública es la función, mientras que la trampa, conocida por
un número restringido de usuarios se denomina clave privada. Así nació el
mundo de Alice, Bob y compañía. Alice y Bob son dos personas que buscan
comunicarse de forma íntegra mientras algunas personas pueden interponerse, escuchando
o incluso alterando el canal de comunicación.
Para descifrar el mensaje el receptor invierte la función utilizando la trampa.
El ejemplo más bello de criptosistema de clave pública y, sin lugar a dudas, el más simple
aparece justo dos años después, en 1978. Se debe a Rivest, Shamir y Adleman de donde
toma el nombre RSA. Se basa en la dificultad de factorizar dos números enteros. La clave
privada está formada por la tripleta (p,q,d) donde p y q son dos
números primos de aproximadamente el mismo tamaño, d es un número entero primo con
p-1 y con q-1. La clave pública se compone del par (n,e). Donde
n=pq y e es el inverso de d módulo (p-1)(q-1), i.e.
ed = 1 mod(p-1)(q-1).
Supongamos que Alice desea enviar un mensaje cifrado con la clave pública
de Bob (n,e). Primero transforma el mensaje en un número m inferior
a n. Después calcula
c = me mod
n,
y envía el resultado c a Bob. Éste, cuya clave pública es (p,q,d),
calcula:
cd mod n =
med mod n =
m.
En el caso de RSA, la función de una sola vía con trampa que se considera
es la función que asocia a un número x<n el valor xe mod n.
Tras el sistema de cifrado RSA, se han desarrollado muchos otros sistemas
de clave pública. Uno de los más utilizados actualmente, y un serio competidor
de RSA es un sistema de cifrado basado en los problemas de cálculo de los logaritmos
discretos.
Sobre el uso moderno de la criptografía
En realidad, el interés de la criptografía de clave pública es el de ocuparse de
muchos problemas de seguridad, y ofrecer una gran flexibilidad. Lo que permite
entre otras cosas encontrar soluciones a los problemas de autentificación:
- La identificación de personas: con la aparición de medios
de comunicación impersonales, Alice quiere estar segura de que la persona
con la que se comunica no hace trampas con su identidad,
es decir que alguien que diga ser Bob lo sea en realidad. Para conseguirlo,
Alice utiliza lo que se llama un protocolo de identificación. Existen
muchos, basándose en los mismos principios que RSA de las propiedades
del logaritmo discreto.
- La autentificación de documentos: una autoridad puede
autentificar documentos por medio de una signatura numérica
. La signatura consiste en añadir
al documento cierto número de bits que se calculan en función del documento
y de la autoridad, y por lo general mediante funciones hash
como MD5 o SHA. Además,
todo el que tenga acceso al documento, debe poder verificar que la signatura
realmente es de la autoridad. Para hacerlo se utilizan los llamados esquemas
de signatura. Uno de los más conocidos es el esquema de signatura
ElGamal que se basa, una vez más, en las propiedades del logaritmo discreto.
Por otro lado, como la criptografía de clave secreta, la criptografía de clave
pública permite elaborar sistemas de cifrado, asegurando la confidencialidad
de las comunicaciones.
Supongamos que Alice desea comunicarse con Bob de forma privada. Alice
encuentra en un directorio la clave pública de
Bob, y cifra el mensaje con esta clave. Cuando Bob recibe el mensaje cifrado,
utiliza su clave privada para descifrar el mensaje y recuperar el texto llano.
Las dos claves juegan papeles completamente distintos, ésta es la razón
por la que se habla de criptosistemas asimétricos, en oposición a los
criptosistemas de clave secreta que utilizan la misma clave para
cifrar que para descifrar y se llaman criptosistemas simétricos.
La criptografía de clave pública presenta otra ventaja sobre la criptografía de clave
secreta. Si n personas desean comunicarse mediante un criptosistema de clave
secreta, cada una de ellas debe disponer de una clave diferente para cada
persona del grupo. Por tanto hace falta poder generar en total n(n-1) claves.
Teniendo en cuenta que n puede ser del orden de varios millares, será
necesario generar ficheros de varios millones de claves. Además, añadir
un miembro al grupo no es sencillo, ya que habrá que generar otrar n
claves para que el nuevo miembro pueda comunicarse con los demás integrantes
del grupo, y después distribuir las nuevas claves a todo el grupo. Por contra,
en el caso de un criptosistema asimétrico, se guardan las n claves
públicas de los miembros del grupo en un directorio.
Para añadir un miembro, basta conque ponga su clave pública en el
directorio.
Clave pública o clave secreta: un compromiso
En el párrafo anterior, se ha visto que la criptografía de clave pública
aporta solución a muchos más problemas que la criptografía de clave
secreta. Entonces nos podemos preguntar cuál es la utilidad de AES.
Existen dos razones fundamentales para escogerlo:
- Por una parte, una razón práctica. En efecto, la mayoría de los sistemas
de cifrado de clave pública son muy lentos. Por ejemplo, RSA es varios
centenares de veces más lento que el AES implementándose en software y es completamente
imposible implementarlo en hardware. Actualmente donde la velocidad
de la transmisión de la información constituye un punto crucial, el algoritmo
de cifrado no puede ser el factor limitante.
- Por otro lado, desde el punto de vista de la seguridad, hay problemas relativos
a la estructura misma de los sistemas de cifrado de clave pública.
Es sorprendente constatar que el tamaño de las claves necesario en criptografía
de clave pública para asegurar un seguridad satisfactoria es mayor que el tamaño
de claves en criptografía de clave secreta. En realidad la noción y la importancia
del tamaño de clave para asegurar la seguridad no tiene sentido más que en el caso
de la clave secreta. De hecho, esos sistemas se basan en la hipótesis de que los
únicos posibles ataques son los llamados ataques exhaustivos (o por fuerza bruta)
que consisten en
enumerar todas las claves posibles. Por ejemplo, en el caso de una clave
de 128 bits, el tamaño del espacio a enumerar es 2128.
Por contra, en el caso de clave pública, el tamaño de clave no tiene sentido más
que cuando se considera el mismo sistema. De hecho, por ejemplo el sistema
RSA de 512 bits es mucho menos seguro que un AES de 128 bits. La única médida
válida para evaluar un criptosistema de clave pública es la complejidad del mejor
ataque conocido. La mayor diferencia es que jamás se está al abrigo
de ataques teóricos. Muy recientemente un grupo de investigadores
ha conseguido factorizar un número de 512 bits. En consecuencia, para tener
una seguridad suficiente para los próximos años, se aconseja generalmente
utilizar números n de 1024 bits.
En cifrado, es mejor entonces utilizar algoritmos de cifrado de clave secreta
cuando sea posible. Una solución completamente interesante y aceptable
es el compromiso elaborado por Zimmermann para concebir PGP. El principio
de cifrado es el siguiente: supongamos que Alice y Bob desean comunicarse
de manera íntegra, utilizando un algoritmo de clave secreta -en el caso de
PGP éste algoritmo es IDEA-.
- Alice y Bob se ponen de acuerdo sobre la clave secreta por un protocolo
de intercambio de claves. Este tipo de protocolos utiliza propiedades de criptografía
de clave pública. Uno de los más conocidos en la materia es el protocolo de
Diffie-Hellman.
- Después se comunican utilizando el algoritmo IDEA, que es público.
Una vez que su conversación ha terminado, rechazan la clave de esa sesión. Tal
sistema combina las ventajas de los dos tipos de criptografía. En general, se considera
que la mayor debilidad se encuentra en el protocolo de intercambio de claves.
Bibliografía
Historia de la criptografía:
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
(N.T. existe una versión en castellano publicada por Editorial Debate en 2000 con
el título "Los códigos secretos").
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
AES :
Criptografía en general :
Formulario de "talkback" para este artículo
Cada artículo tiene su propia página de "talkback". A través de esa página puedes enviar un comentario o consultar los comentarios de otros lectores
2002-05-20, generated by lfparser version 2.21




